All måling er beheftet med feil.
Typer av feil:
a. Representasjonsfeil: Den målte størrelse svarer ikke nøyaktig til den størrelsen vi øsker å bestemme. Dette kan f. eks. inntreffe ved diametermåling på en oval stamme.
b. Målefeil: Den målte størrelsen bestemmes ukorrekt. Dette skyldes enten observatøren eller det instrument han bruker, eller begge deler.
Både a og b kan være av systematisk (ensidig), eller tilfeldig art. Systematiske feil kan f. eks. forekomme ved diametermåling når klavearmen er skjev. Slike feil er uavhengig av antall målinger, men kan elimineres – eller reduseres – når en blir klar over dem. Tilfeldige feil fordeler seg som regel symmetrisk omkring den riktige middelverdi, overensstemmende med den normale fordelingslov. Denne funksjon
finnes tabulert i en rekke lærebøker. Den tilfeldige feil på en måling kalles spredningen eller middelavviket. Kjenner en spredning eller den estimerte verdi av denne (S), er det mulig å beregne hvor mange målinger som må utføres for at middeltallet skal være bestemt med en
viss sikkerhet. Nøyaktigheten av middeltallet uttrykkes ved middelfeilen Sx.
Spredningen beregnes av formelen 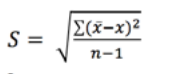
og middelfeilen av formelen: 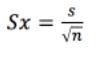
hvor:
x = størrelsen av den enkelte observasjon,
x = aritmetisk gjennomsnitt av alle observasjonene,
n = antall observasjoner.
Variasjonskoeffisienten er spredningen i % av middeltallet (aritmetisk gjennomsnitt)![]()
En slik beregning av middelfeilen forutsetter at resultatet av hver observasjon er uavhengig av resultatet av alle andre observasjoner. Når det gjelder å bedømme de enkelte målinger og måleinstrumenter, vil denne forutsetning som regel være oppfylt.